こんにちは。メルカリのR4DでProfessional Internshipをしている@yonesuke です。
この記事ではD-Waveの量子アニーリングマシンを実際に使って行ったことについて紹介したいと思います。
背景
最近巷では量子が来る!なんて言われ方もするほど量子という言葉が付くものには注目が集まっています。そんななか、メルカリのインターンでD-Wave社の量子アニーリングマシン*1を用いて組合せ最適化問題を解くことが出来る!というのに惹かれて今回の応募しました。
本ブログでは量子コンピュータやD-Waveで使われる言葉が少しだけ使われています。わからない用語があった場合はこちらのページで調べてみるといいかもしれません。
D-Waveが解ける問題
D-Waveの量子アニーリングマシンはイジング模型のハミルトニアンの基底状態を求めることを目標としています。ここでイジング模型のハミルトニアンは次の形で表されるものを言います。
begin{align}
H(sigma)=-sum_{i< j}J_{ij}sigma_{i}sigma_{j}-sum_{i=1}^{N}h_{i}sigma_{i}
end{align}
ここで(sigma)は変数の組({sigma_{1},sigma_{2},cdots,sigma_{N}})で、各(sigma_{i})は(pm 1)の2つの値をとるイジングスピンと呼ばれるものです。
(J_{ij})はスピン同士の相互作用を表し、(h_{i})は各スピンへの局所磁場を表します。
イジング模型のハミルトニアンの基底状態を求める問題は、与えられた({J,h})に対してハミルトニアンを最小にする(sigma)を求める問題、という風に言うことが出来ます*2。
相互作用をエッジとしてグラフを書く事ができます。現在のD-Wave 2000QのQPUではこの相互作用のグラフとしてキメラグラフを採用しているので、解きたい組合せ最適化問題の相互作用グラフが必ずしもQPUに乗るとは限らないのです。
その場合は、1つのイジングスピンを複数個に複製し、QPUへマッピングするという操作を行います。
この操作を埋め込み*3と言います。
最適化問題をイジング模型で表現して出来るグラフには、キメラグラフのノードより高い次数のノードが発生する事が多く、遠くの場所との相互作用を入れざるを得なくなるため、埋め込みは必須のテクニックになります。
イジング模型に落とし込める問題の1つに分割問題があります。
分割問題は自然数の集合({n_{1},n_{2},cdots,n_{N}})を集合AとBに分けて、それぞれの集合の数の和を等しくなるようにする問題です。
例えば、
begin{align}
{3,5,8}
end{align}
については、
begin{align}
{3,5}, {8}
end{align}
とすれば良いことがわかります。
分割問題はNP完全という問題のクラスに属していて、大きいサイズの問題を効率的に解く方法は現在知られていません。
実は分割問題はイジング模型で簡単に表すことが出来ます。
ハミルトニアンを
begin{align}
H=left(sum_{i=1}^{N}n_{i}sigma_{i}right)^{2}=sum_{i,j=1}^{N}n_{i}n_{j}sigma_{i}sigma_{j}
end{align}
と設定します。
このハミルトニアンを最小にする最適解(sigma)において、
(sigma_{i}=1)ならば(n_{i})は集合A、(sigma_{i}=-1)ならば(n_{i})は集合Bに属する、
ということにすれば最適解が求まることがわかります。
実際の組合せ最適化問題を考える場合、(pm 1)ではなく(0,1)で問題を定式化することがあります。
その場合、(0,1)変数に関する2次の制約なし問題(QUBO)を考えます。QUBOは、
begin{align}
&mathrm{min. quad} x^top Qx \
&mathrm{s.t. quad} x in {0, 1}^n
end{align}
の形で定式化されます。
実はQUBOの問題はイジング模型のハミルトニアンの基底状態を求める問題に等価に変形出来る*4ことが知られています。
D-WaveのAPIはQUBOの行列(Q)を投げることでも問題を解いてくれます。
Graph Golf
このインターンが始まるにあたってGraph Golf: The Order/degree Problem Competitionの問題を解きたいと思いました。
Graph Golfは次のような問題を考えるコンペティションです。
与えられた頂点数と次数に対して、直径と平均距離を最小にするグラフ*5を求めよ。
この問題を考えるためにはじめに与えられた頂点数と次数に対する正則グラフを生成することを考えました。生成に際して、グラフの隣接行列を用いました。
隣接行列はグラフの頂点間に辺が伸びていれば、対応する行列の要素を1に、辺がなければ0にするような行列のことです。
例えば次のグラフを考えてみましょう。
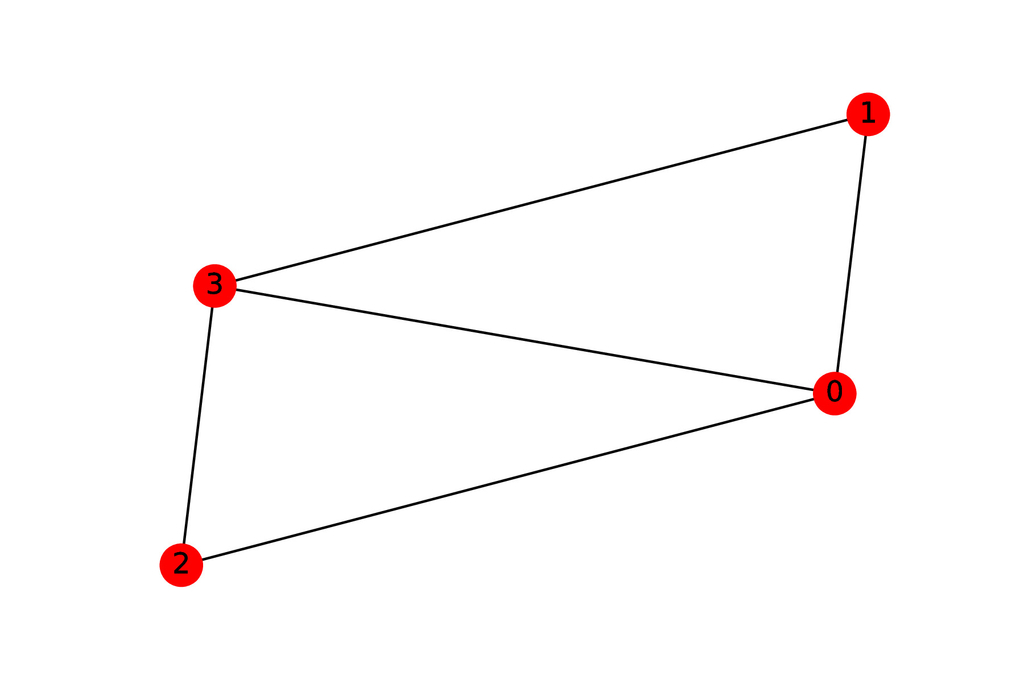
このグラフは
- 頂点0からは頂点1、2、3に辺が伸びている。
- 頂点1からは頂点0、3に辺が伸びている。
- 頂点2からは頂点0、3に辺が伸びている。
- 頂点3からは頂点0、1、2に辺が伸びている。
となっています。これより、隣接行列 (A)は
begin{align}
A=
begin{pmatrix}
0 & 1 & 1 & 1\
1 & 0 & 0 & 1\
1 & 0 & 0 & 1\
1 & 1 & 1 & 0
end{pmatrix}
end{align}
となることがわかると思います。
正則グラフの生成に際し、隣接行列の各要素を変数とする組合せ最適化問題を考えます。
今回は、
- 自分の頂点に伸びるような辺(ループ)は考えない。
- 無向グラフを考える。
という条件に注意すると、考えるべき隣接行列の変数の数は頂点数(n)に対して、$$
frac{n(n-1)}{2}
$$
になります。例えば頂点数6のグラフを考える場合変数の数は15になります。
これは隣接行列で見てみると次のようになります。
begin{align}
A=
begin{pmatrix}
0 & x_{1} & x_{2} & x_{3} & x_{4} & x_{5}\
x_{1} & 0 & x_{6} & x_{7} & x_{8} & x_{9}\
x_{2} & x_{6} & 0 & x_{10} & x_{11} & x_{12}\
x_{3} & x_{7} & x_{10} & 0 & x_{13} & x_{14}\
x_{4} & x_{8} & x_{11} & x_{13} & 0 & x_{15}\
x_{5} & x_{9} & x_{12} & x_{14} & x_{15} & 0
end{pmatrix}
end{align}
各変数(x_{i})は(0,1)の値を取ります。
この隣接行列に対して正則グラフであるための条件は、各頂点から伸びる辺の本数が(d)になる、ということです。
これは各行の和が(d)になることと同値です。
変数の関数を何かしらの定数と一致させたいときには引き算して2乗すると最小化問題として扱え、QPUに載せることが出来るようになります。これを踏まえるとハミルトニアンは
begin{align}
H=&(x_{1}+x_{2}+x_{3}+x_{4}+x_{5}-d)^{2}\
+&(x_{1}+x_{6}+x_{7}+x_{8}+x_{9}-d)^{2}\
+&(x_{2}+x_{6}+x_{10}+x_{11}+x_{12}-d)^{2}\
+&(x_{3}+x_{7}+x_{10}+x_{13}+x_{14}-d)^{2}\
+&(x_{4}+x_{8}+x_{11}+x_{13}+x_{15}-d)^{2}\
+&(x_{5}+x_{9}+x_{12}+x_{14}+x_{15}-d)^{2}
end{align}
となります。これは変数(x_{i})に関する2次式で表されていて、QUBOの形で立式できることがわかりました。
(d=3)としてD-Waveに解かせると解の1つとして次が得られました。確かに正則グラフになっていることが確認できますね!
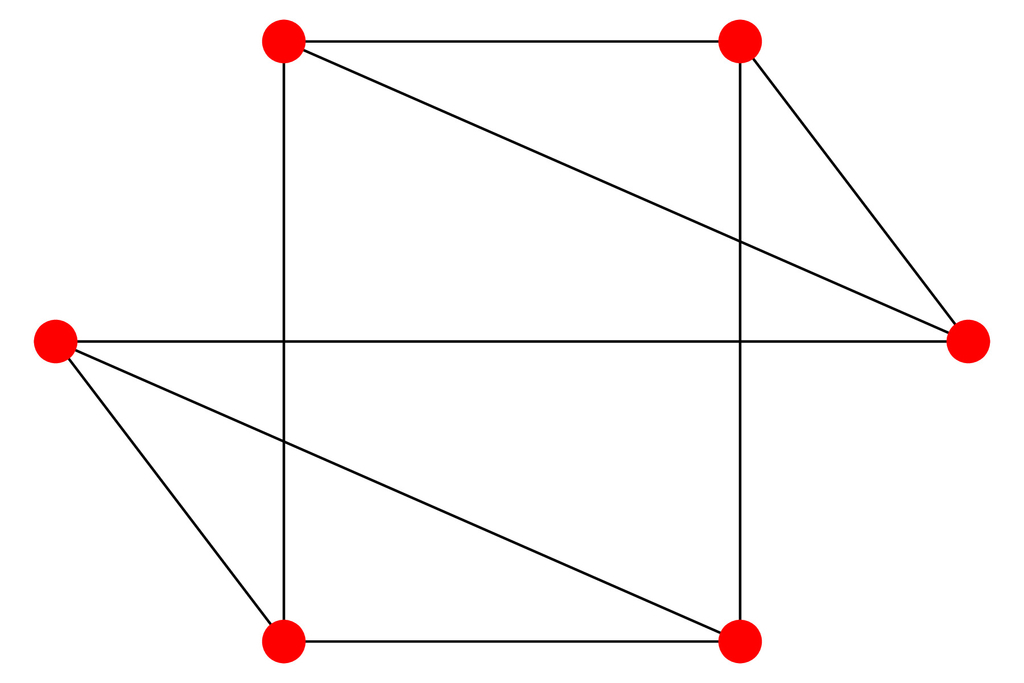
次に直径と平均距離を最小化することを考えました。インターン中に考えたものとして次の2つがあります。
-
考えるグラフの隣接行列(A)とその直径(k)の間には次の関係があることが知られています。
begin{align}
left(sum_{m=1}^{k}A^{m}right)_{i,j}>0,quad for all (i,j)
end{align}
これを目的関数として取り込むことを考えました。
すなわち、与えられた頂点数、次数について、直径(k)のグラフがほしいときに、
(left(sum_{m=1}^{k}A^{m}right)_{i,j})を最大化すれば、
与えられた頂点数、次数、直径を満たすグラフが得られるのではないか? -
グラフの直径をダイレクトに評価するのではなく、直径や平均距離に影響を与える数を小さくしてはどうか??と考えました。
やや直観的な議論になりますが、グラフの中に小さな閉路(三角形や四角形の閉路)がたくさんあると、
頂点間を移動するときに近傍の頂点を移動することが多くなるので遠くの頂点に移動する際に
経路長が長くなってしまい、結果的に直径が大きくなってしまう、と思えます*6。
なので、グラフに含まれる三角形や四角形の数を減らそう、と考えました。
グラフ(G)内に存在する三角形閉路の数(c_{3}(G))、四角形閉路の数(c_{4}(G))は、隣接行列(A)を用いると、
begin{align}
c_{3}(G)&=frac{1}{6}textrm{tr}left(A^{3}right)=frac{1}{6}sum_{i,k,l}a_{ik}a_{kl}a_{li}\
c_{4}(G)&=frac{1}{8}left(textrm{tr}left(A^{4}right)-2q-2sum_{ine j}a^{(2)}_{i,j}right)
end{align}
と書けます
*7。
ここで、(q)はグラフの辺の本数、(a^{(2)}_{i,j})は隣接行列の2乗の( (i,j))成分を表します。
この(c_{3}(G))、(c_{4}(G))の値を最小化すれば、直径が小さいグラフが得られるのではないか?
しかし、上の2つのアイデアはどちらもうまくいきませんでした。
例えば(c_{3}(G))を計算させようとすると3次の多項式が現れ、このままではD-Waveに載せる事ができません。
この問題を回避するために3次式を2次式以下にする必要があり、それに伴って大量の補助変数を導入しないといけなくなります
*8。
この場合だと(i,k,l)に関する和を取っているので(n^{3})個の補助変数が必要になります。
これではD-Wave 2000QのQPUに載せることが出来ません!!
直径を評価するところで2週間近く悩みましたがこれ以外にあまり上手い評価を考えることが出来ませんでした。
なにか良いアイデアがある方はぜひ教えてください!!
実際にD-Waveを使ってみた感想
今回のインターンでは、一ヶ月間組合せ最適化問題を解いてみる、という観点からD-Waveを触りました。
具体例で挙げた分割問題をD-Waveで解かせてみたところ、最適解を出力してくれました。
また、分割問題は2つの集合に分ける問題でしたが、これを3つの集合に分ける問題に拡張した場合にも最適解が得ることが出来たのは驚きました。
一方で、D-Waveはどんな組合せ最適化に対しても良い解を出力してくれる、というわけではありません。
むしろ、多くの問題であまり良い最適解を得ることが出来ませんでした。
その過程で苦労したことをいくらかまとめてみました。
今後D-Waveを使って組合せ最適化問題を解く人のためになれば幸いです。
- D-Waveで組合せ最適化問題を解かせるときは制約条件を罰金項として目的関数の後ろにつけるのですが、
実際に得られた解を見てみると制約条件を満たさないような解が出てくることが往々にしてあります。
そのため、制約条件を満たすような解を見つけるためにいくらかの試行錯誤をする必要があり、ここらへんは非常に心が折れるような作業をする必要があります*9。
単純に試行回数を増やす、という手段もありますが、そこらへんはお金との相談ですね。。。 - 最初に少しまとめましたが、D-Waveの相互作用のグラフはキメラグラフになっています。そのため、QPUに埋め込めることが出来る最大の完全グラフの頂点数はたったの64です。2048qubitあるからと言って、2048変数の組み合わせ最適化問題を解くことが出来るわけではない、ということに注意する必要があります。
キメラグラフにうまく載る相互作用を持つ問題で、古典のコンピューターで効率的に解けないような問題が見つかればD-Wave的にもハッピーで良いですね。 - これは量子アニーリングそもそもに関することですが、定式化するためには0,1もしくは1,-1の2値を持つ変数を使わないと行けなくて、しかもその2次式に関する問題しか扱うことが出来ない、ということです。定式化した問題に3次式以上のものが出てきたときは2次式に落とし込むための補助変数を導入する必要があります。問題を定式化する段階で2次式しか出てこないようにうまいことしてやるのが良いでしょう。
現状のD-Wave 2000Qだとまだまだ出来ることより出来ないことのほうが多いように感じました。
理論的にも解明されていないこともたくさんあって、実用に耐えうるものではありません。
裏を返せば、研究がどんどん進む分野であることは間違いないです。
今後、量子アニーリングに関する研究が進んで、現状よりも良い最適解が求まり、実生活が最適化されることを期待しています。
*1:ここらへんの名前は非常にsensitiveなところであり、まだ議論の最中です。http://tomoyukimorimae.web.fc2.com/realQC.pdf が参考になります。
*2:参考文献として次がおすすめです。西森秀稔 & 大関真之. (2018). 量子アニーリングの基礎. 東京, 日本: 共立出版.
*3:https://qard.is.tohoku.ac.jp/T-Wave/?glossary=%E5%9F%8B%E3%82%81%E8%BE%BC%E3%81%BF
*4:QUBOの変数(x_{i})を用いて(sigma_{i}=2x_{i}-1)と変換することでイジングスピンに変換することが出来ます。
*5:与えられた次数に対するグラフというのはその次数に関する正則グラフ、ということです。
*6:http://sucrose.hatenablog.com/entry/2014/12/21/202546
*7:Harary, F., and Manvel, B. (1971). On the number of cycles in a graph. Matematický časopis, 21(1), 55-63.
*8:3次式を2次式に落とし込むテクニックとして次があります。0,1変数の(x,y,z)に対して3次式(xyz)は
begin{align}
xyz=max_{win{0,1}}w(x+y+z-2)
end{align}
となります。
ただ、これは(max)関数を用いた意味において等価なので場合によってはD-Waveがきちんと計算してくれないことに注意する必要があります。
*9:慣れるとササッと出来るようになるらしいですが1ヶ月では難しかったです。。。





